Опорная гиперплоскость
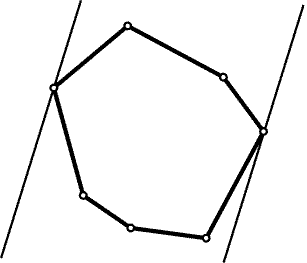
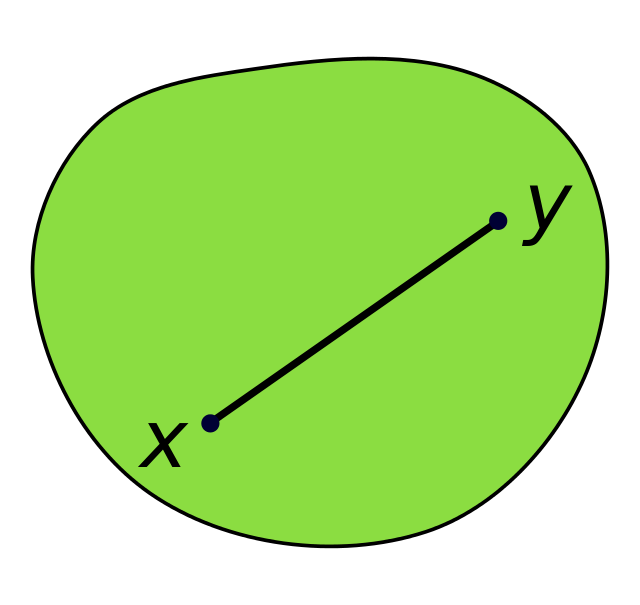
Выпуклость, вогнутость [convexity, concavity]. В математике рассматриваются, во-первых, выпуклые области или, что то же самое в теории множест в — выпуклые множества ; во-вторых, выпуклые функции. Через каждую точку ее границы можно провести опорную прямую , которая не рассекает эту область. Эти понятия переносятся с двумерного пространства плоскости на многомерное.





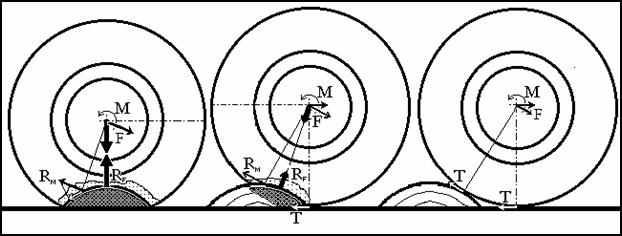
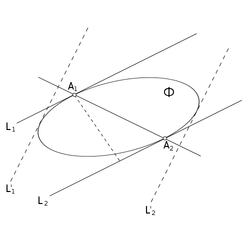


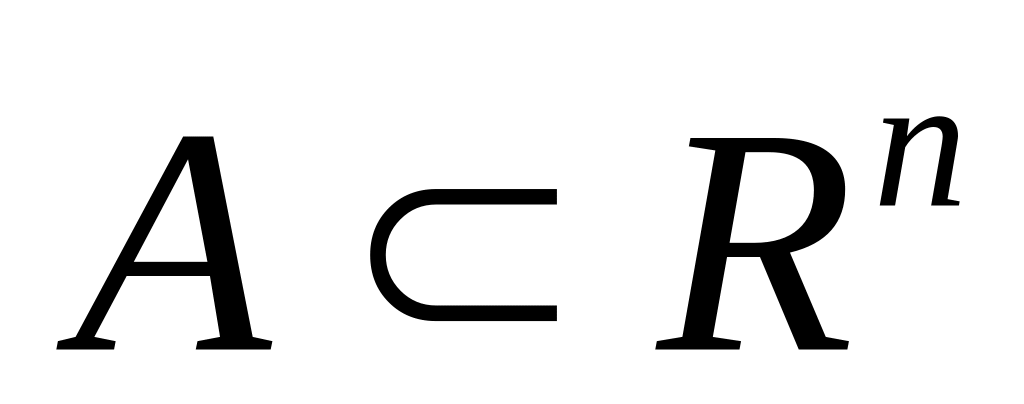



Опорная прямая — прямая , содержащая точку фигуры, но не разделяющая какие-либо две точки на ней [1]. Другими словами, C полностью лежит в одной из двух замкнутых полуплоскостей , на которые делит плоскость прямая L, и хотя бы одна точка кривой принадлежит L. В данной точке кривой может быть множество опорных прямых. Если существует касательная в данной точке, то она является единственной опорной прямой в этой точке, при условии что прямая не разделяет кривую.






Круг и шар. Вильгельм Бляшке М. Тираж экз. Загрузить Mb djvu 2. Наряду с этим рассматриваются свойства выпуклых тел.