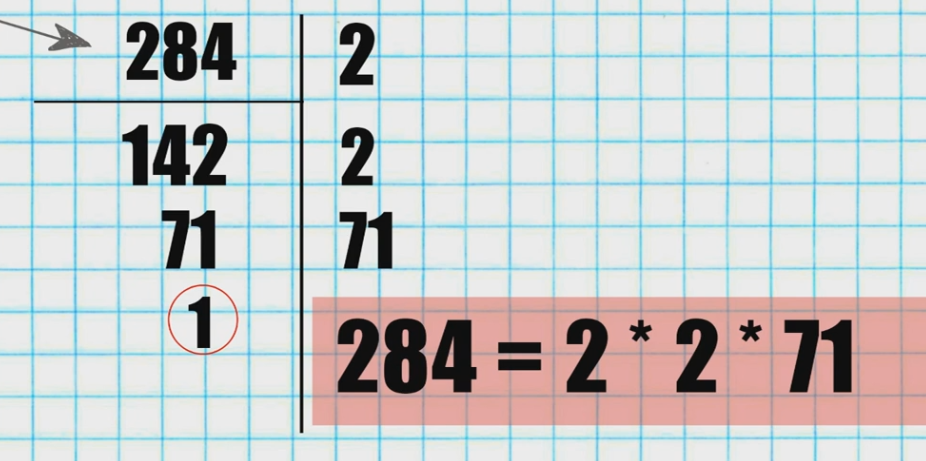Признаки делимости на натуральные числа
Сегодня мы расскажем про делители и кратные натуральных чисел. Вам будет интересно узнать про признаки делимости чисел и деление всех чисел на простые и составные. Мы рассмотрим разложение на простые множители и научимся находить наибольший общий делитель и наименьшее общее кратное нескольких чисел. Предположим, у нас с вами есть 6 яблок, и мы хотим разделить их поровну между двумя нашими друзьями.











Признаки делимости на. Не могу поверить, что каждый раз нужно делить в столбик, чтобы узнать делится ли одно число на другое. Во многих случаях удобно пользоваться критерием, который определяет необходимое и достаточное условие делимости произвольного натурального числа на данное натуральное число. В простонародье этот критерий называют признаком делимости на. Различают общие признаки делимости, которые устанавливают для произвольного значения , и частные — для конкретных значений. Общий признак делимости определяет правило, по которому по цифрам числа можно судить о делимости его на другое число.


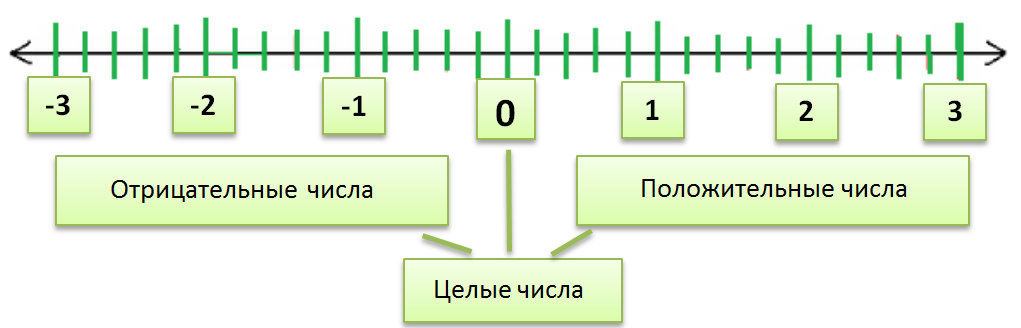

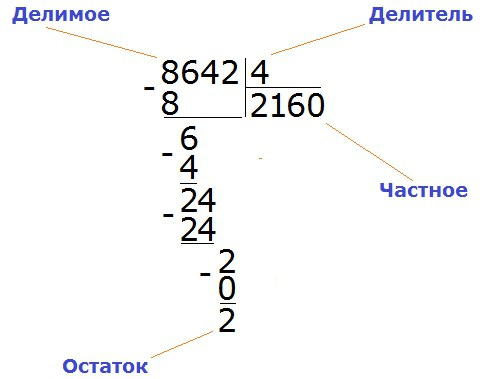
Для упрощения деления натуральных чисел были выведены правила деления на числа первого десятка и числа 11, 25, которые объединены в раздел признаков делимости натуральных чисел. Ниже приводятся правила, по которым анализ числа без его деления на другое натуральное число даст ответ на вопрос, кратно ли натуральное число числам 2, 3, 4, 5, 6, 9, 10, 11, 25 и разрядной единице? Натуральные числа, имеющие в первом разряде цифры оканчивающиеся на 2,4,6,8,0, называются четными. На 3 делятся все натуральные числа, сумма цифр которых кратна 3. На 4 делятся все натуральные числа, две последние цифры которых составляют нули или число, кратное 4. На 6 делятся те натуральные числа, которые делятся на 2 и на 3 одновременно все четные числа, которые делятся на 3.