Начертательная геометрия 1 курс ДВГУПС
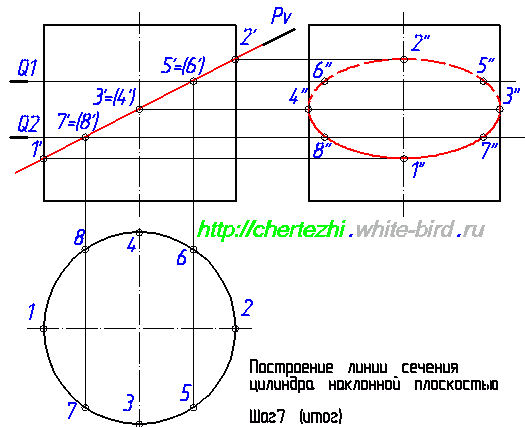
Построение сечения цилиндра. Построение сечения конуса. Определение натуральной величины сечения. Контрольные задания по теме: Рабочая тетрадь задача 68 , задача Цилиндром будет называться геометрическое тело, полученное при ограничении цилиндрической поверхности двумя параллельными плоскостями - основаниями цилиндра. Если в основании цилиндра лежит окружность, а образующая перпендикулярна основанию, то цилиндр называется прямым круговым.





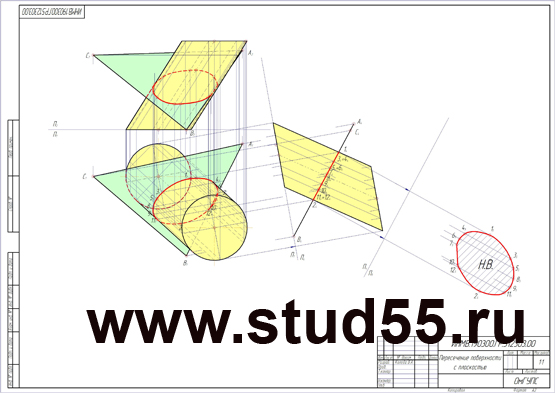
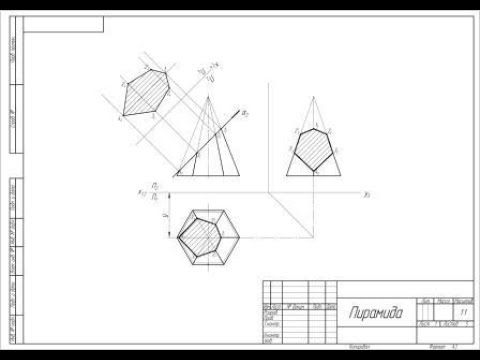

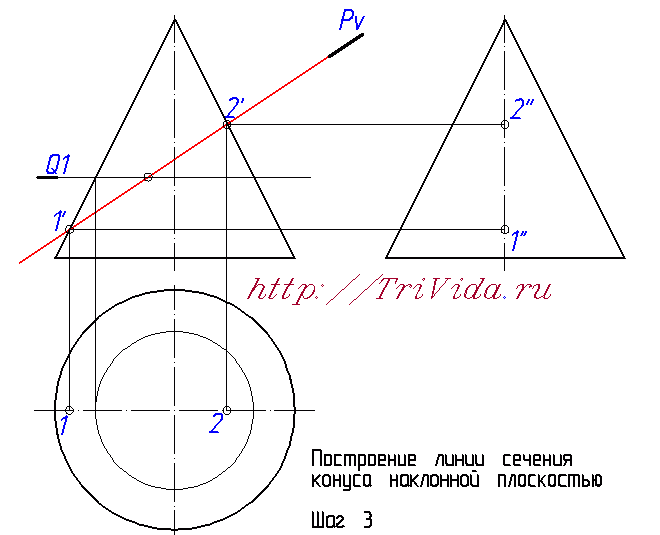


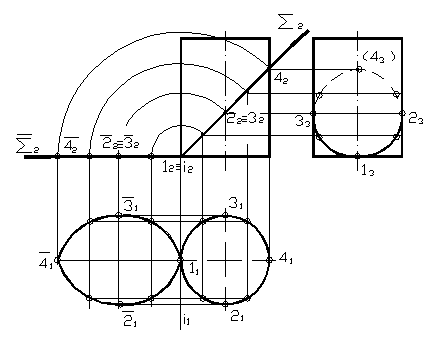

Пересечение поверхности плоскостью (построение сечения)
Под разверткой многогранной поверхности подразумевают плоскую фигуру, составленную из граней этой поверхности, совмещенных с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней — плоских многоугольников. Способ нормального сечения применяется для развертки призматических гранных поверхностей.
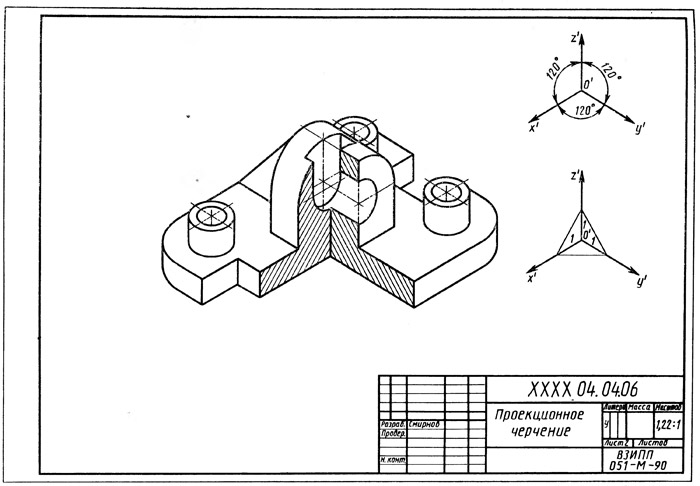
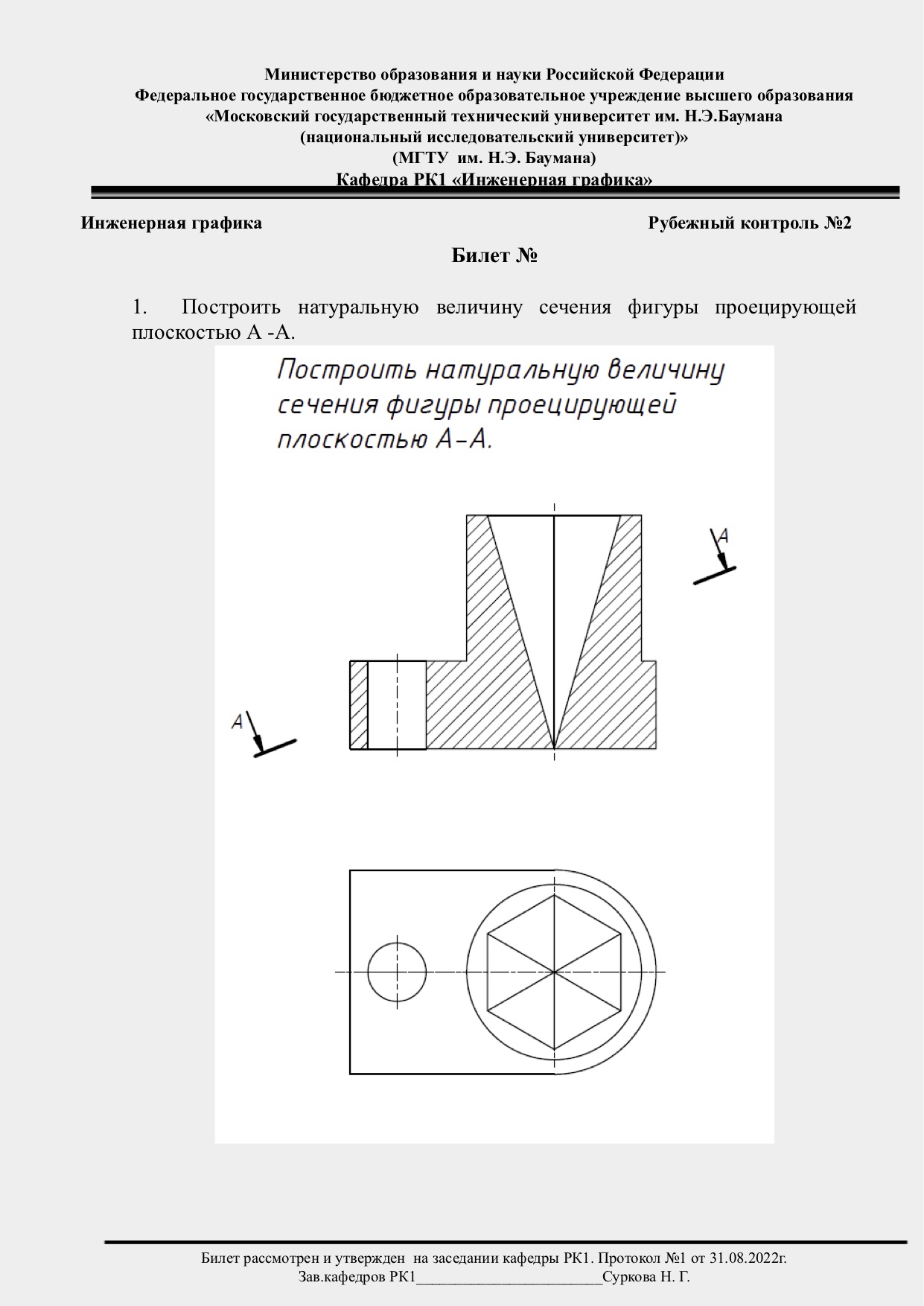
- Построить три проекции комбинированного геометрического тела; 2. Три проекции фигуры сечения геометрического тела фронтально-проецирующей плоскостью;.
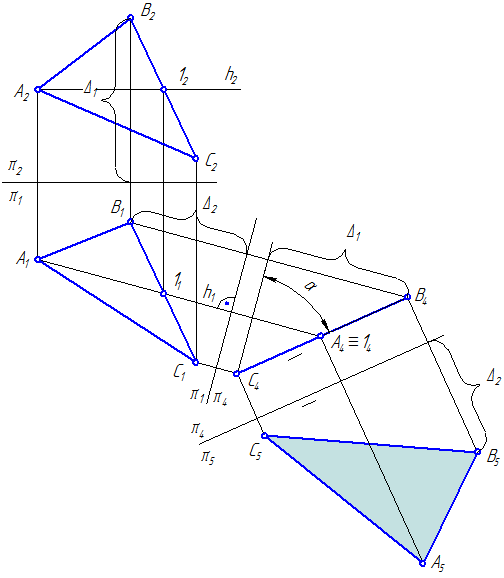
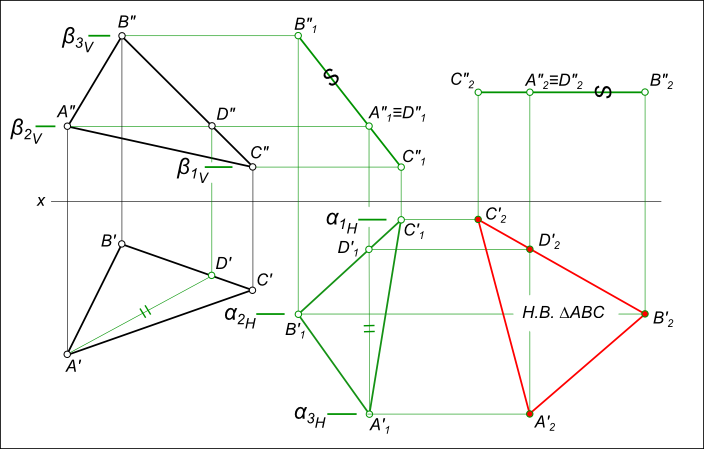
- В курсах начертательной геометрии рассматривается ряд способов нахождения истинной величины сечения фигуры, в частности, способ совмещения.
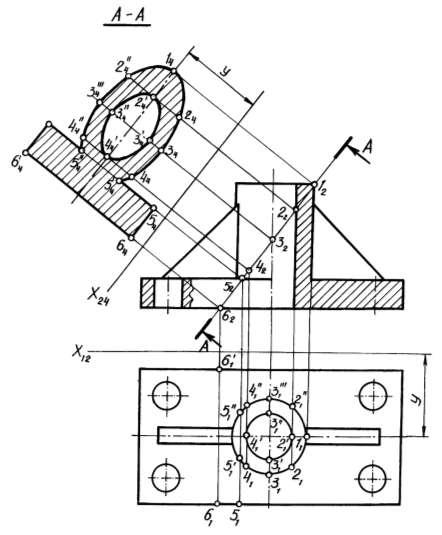
- При построении натурального вида сечения деталь пересекают фронтально проецирующей плоскостью рис. Линию сечения показывают разомкнутой линией с указанием стрелками направления взгляда и обозначают ее с двух сторон одинаковыми прописными буквами русского алфавита.
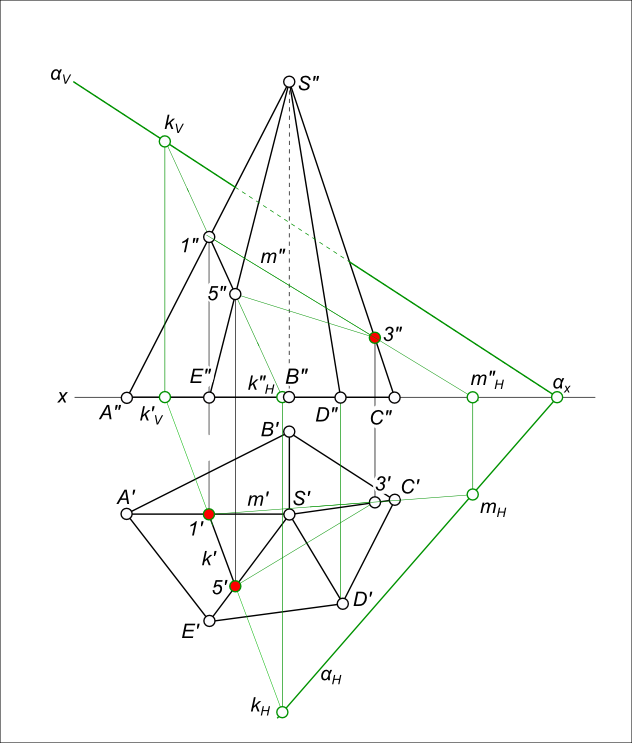
- При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.
- Сечением призмы является плоская фигура, т. Построение натуральной величины сечения начинается с построения собственно сечения - пересечения рёбер призмы с секущей плоскостью.
- В машиностроительных чертежах встречаются детали, для выявления внутренней конструкции которых следует выполнить наклонное сечение или разрез рис. Построение изображений должно быть максимально упрощено, поэтому в качестве секущих плоскостей всегда используют плоскости частного положения.





При пересечении поверхности или какой-либо геометрической фигуры плоскостью получается плоская фигура, которую называют сечением. Сечение поверхности плоскостью в общем случае представляет собой кривую или прямую, если пересекаются плоскости , принадлежащую секущей плоскости. Определение проекций линий сечения следует начинать с построения опорных точек - точек, расположенных на очерковых образующих поверхности точки, определяющие границы видимости проекций кривой ; точек, удаленных на экстремальные максимальное и минимальное расстояния от плоскостей проекций. После этого определяют произвольные точки линии сечения.