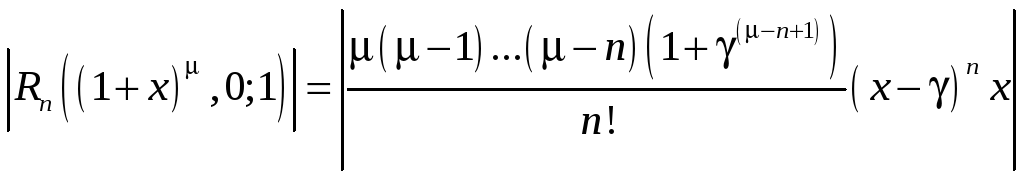19.Формула Тейлора. Остаточный член в форме Пеано и в форме Лагранжа.
Вычисление с погрешностью. Как узнать сколько членов брать для вычисления к примеру с точностью? В учебнике написано,что надо решить какое-то неравенство с остаточным членом,плохо это понял. Что за ряд нужно применить?








Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше. Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике. Выше мы установили формулу Тейлора с остаточным членом в общей форме. Здесь мы установим другие возможные представления для остаточного члена. Два из них могут быть получены в качестве частных случаев из общей формы.




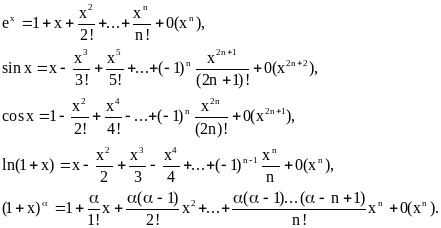



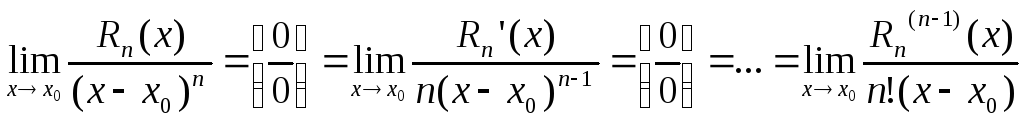

Конев В. Дифференцирование функций. Разделы курса Примеры Калькулятор. Пределы Неопределенные интегралы Определенные интегралы Несобственные интегралы. Остаточный член в форме Лагранжа. Для контроля погрешности вычислений, основанных на использовании формулы Тейлора, полезно располагать различными формами представления остаточного члена, наиболее употребительной из которых является форма Лагранжа,.