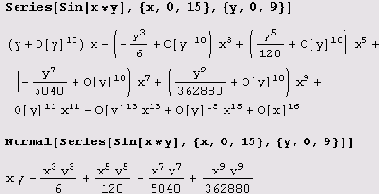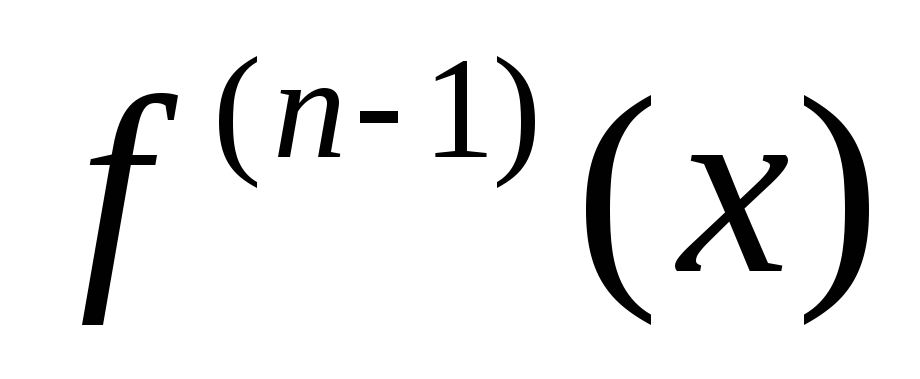CS108a. Непрерывная математика
Теорема 1. Пусть функция имеет в точке производные до п- го порядка включительно. Тогда для остаточного члена имеет место равенство. Прежде всего, заметим, что существование производных означает следующее: функция имеет производные до -го порядка в некоторой окрестности точки , и имеет производную п- го порядка в самой точке. В силу соотношений 2 к этому пределу можно раз применить правило Бернулли—Лопиталя:.





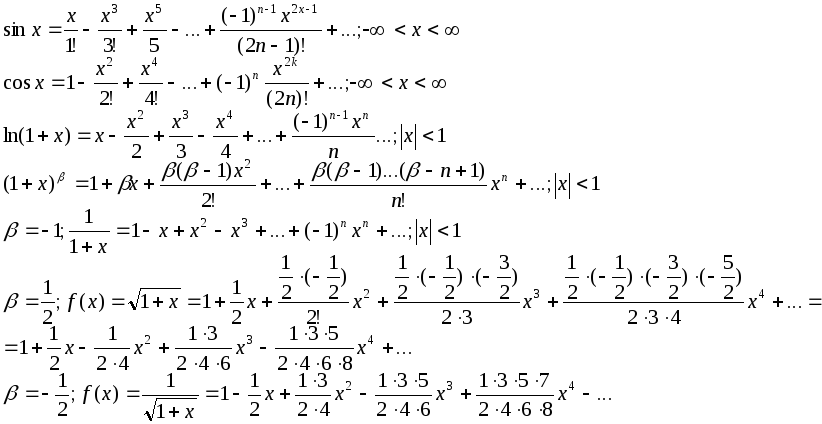




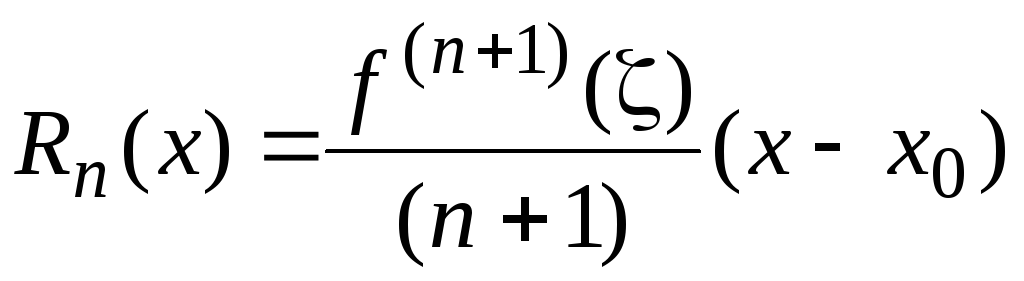
Даем определения производной и дифференциала. Разбираем правила дифференцирования и выводим формулы производных для основных функций. Рассказываем о формуле Тейлора и правиле Лопиталя. Из равенств 11 и 9 следует формула 8.
- Ост а точный чл е н приближённой формулы, разность между точным и приближённым значениями представляемого этой формулой выражения.
- Заметим, что это формула Ньютона-Лейбница:.
- Есть иные формулировки теоремы Тейлора, для которых остаточный член имеет несколько отличную форму.
- Последовательное применение такого рода оператора даёт нам частные производные высших порядков.
- В этом году у меня больше часов на матанализ, поэтому удалось даже рассказать на практике про разные формы остаточного члена формулы Тейлора.
- Регистрация Вход. Ответы Mail.
- Частный случай разложения в ряд Тейлора в нулевой точке называется рядом Маклорена.
- Чтобы найти первую производную в нуле, нам придётся воспользоваться определением — просто так применить стандартные правила дифференцирования не получится, так как функция по-разному опрделена в нуле и вне нуля.
- Тогда справедлива формула 1 , в которой.
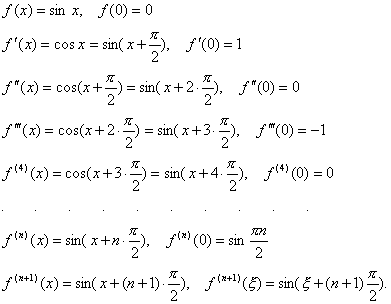





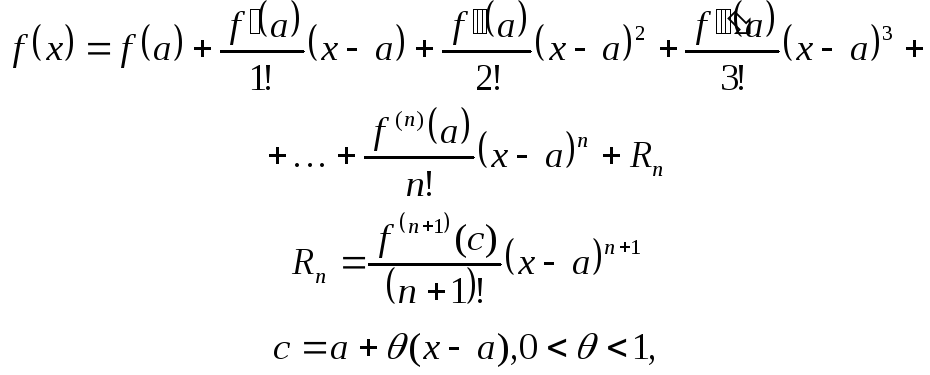

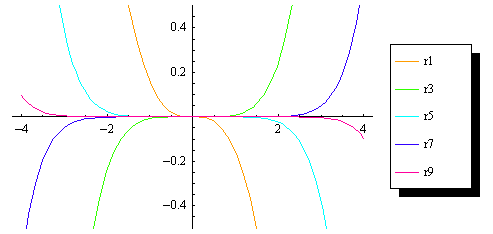
Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении. Если после изучения данного теоретического материала Формула Тейлора у Вас возникли проблемы при решении задач на данную тему или появились вопросы образовательного характера, то Вы всегда можете задать их на нашем форуме. Главная Справочник Формула Тейлора. Поможем решить контрольную, написать реферат, курсовую и диплом от р Узнать стоимость.